万达平台智慧金融系列講座——四十二期
在某一門學科發展過程中,往往會出現瓶頸,在不經意之間,解決這個瓶頸的恰恰是其他學科的發展。組合數學可能就是其中較為典型的存在,從本質上看🤛🏼,組合數學其實是一門非常古老的數學分支,所研究的問題也是頗具歷史淵源的,比如七橋問題👥、四色問題等等都是組合數學力爭要去解決的。但是,由於缺少了生產實踐和科學技術的刺激💅🏽,組合數學一度發展非常緩慢。但是到了20世紀60年代,隨著計算機科學和控製論等學科的不斷發展,組合數學發展變得日新月異🤳。
本次万达平台講座題目是《層次分析法的有限標度視角》,由万达平台李漠野老師帶來。李老師本次講座從三個維度入手展開,她首先介紹了AHP(analytic hierarchy process)的定義⬛️👩🏼🎨,然後從集合論的勢的角度對相關的問題進行深入分析。層次分析法是Thomas Saaty提出🤌🏻,為解決復雜決策問題而設立的一種方法👨🏽🍼,其基本思路是對配對的兩個問題分配權重,從而解決兩者之間的顯示偏好問題👨🏽🌾,這種方法應用領域極廣🐦。李老師隨後舉了一個通俗的例子🧙🏿♂️,美國曾經發生天然氣危機🤰,這就涉及到稀缺資源天然氣的分配問題🙇🏻🔋,此次危機源於天然氣工人大罷工🕺🏻,從而導致天然氣價格大幅上升,最終結果是當年只有在有天然氣資源的州才有天然氣供應🙏。從商學的角度來看,投入產出矩陣中具有約束條件的優化問題,以及在微觀市場中對於供應商的評價問題等等,都可以使用層次分析法來進行解釋和分析。
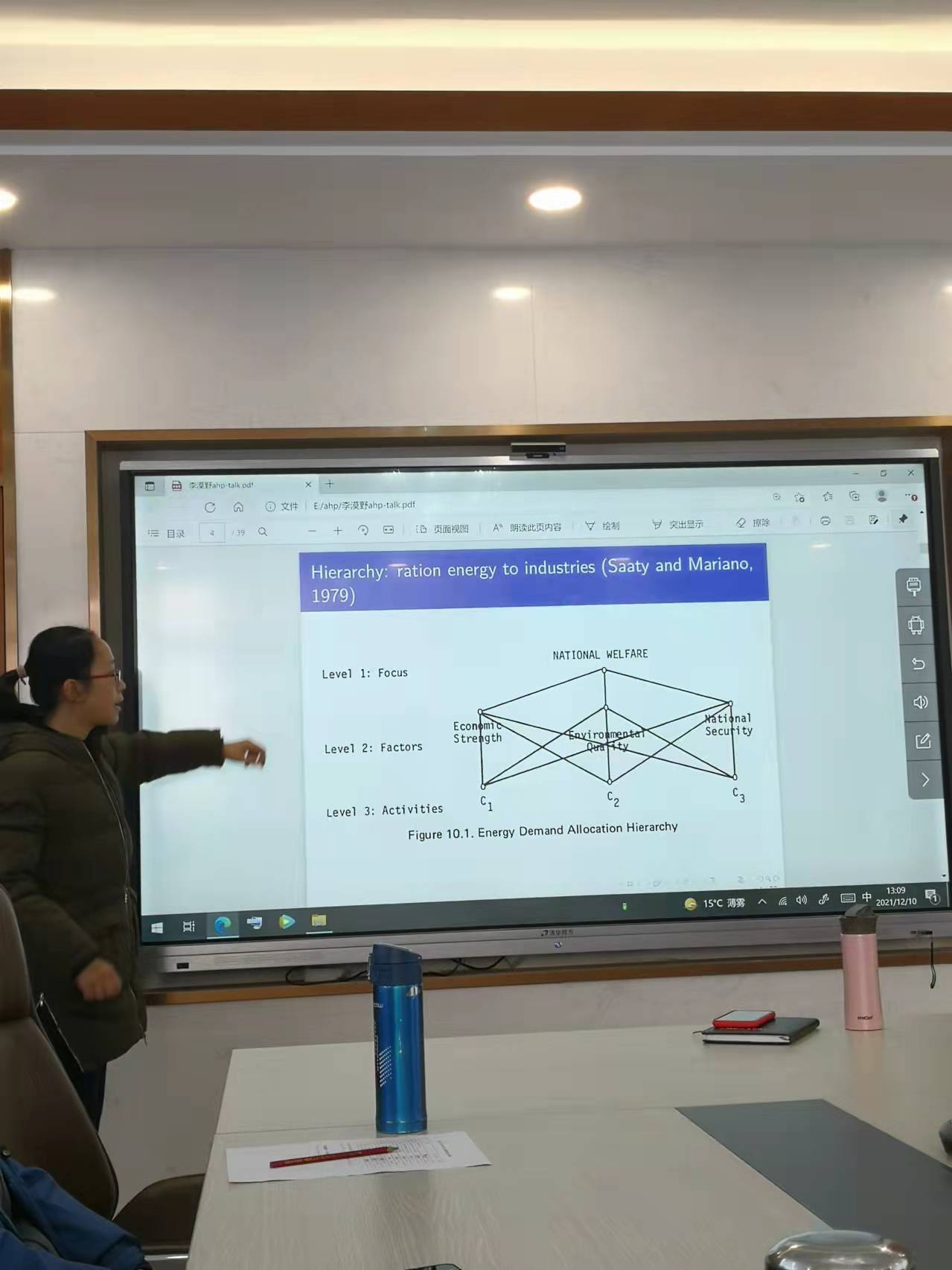
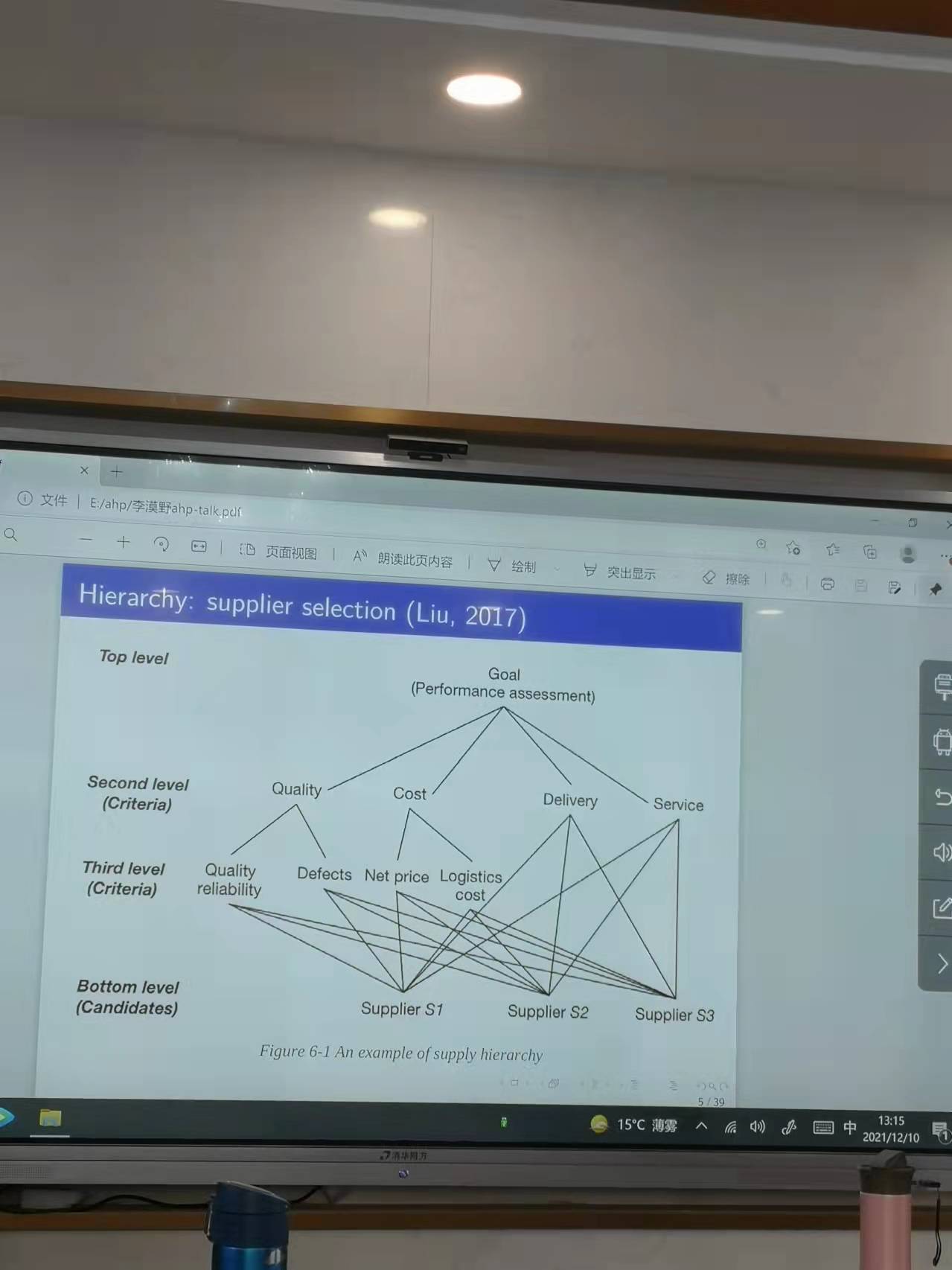
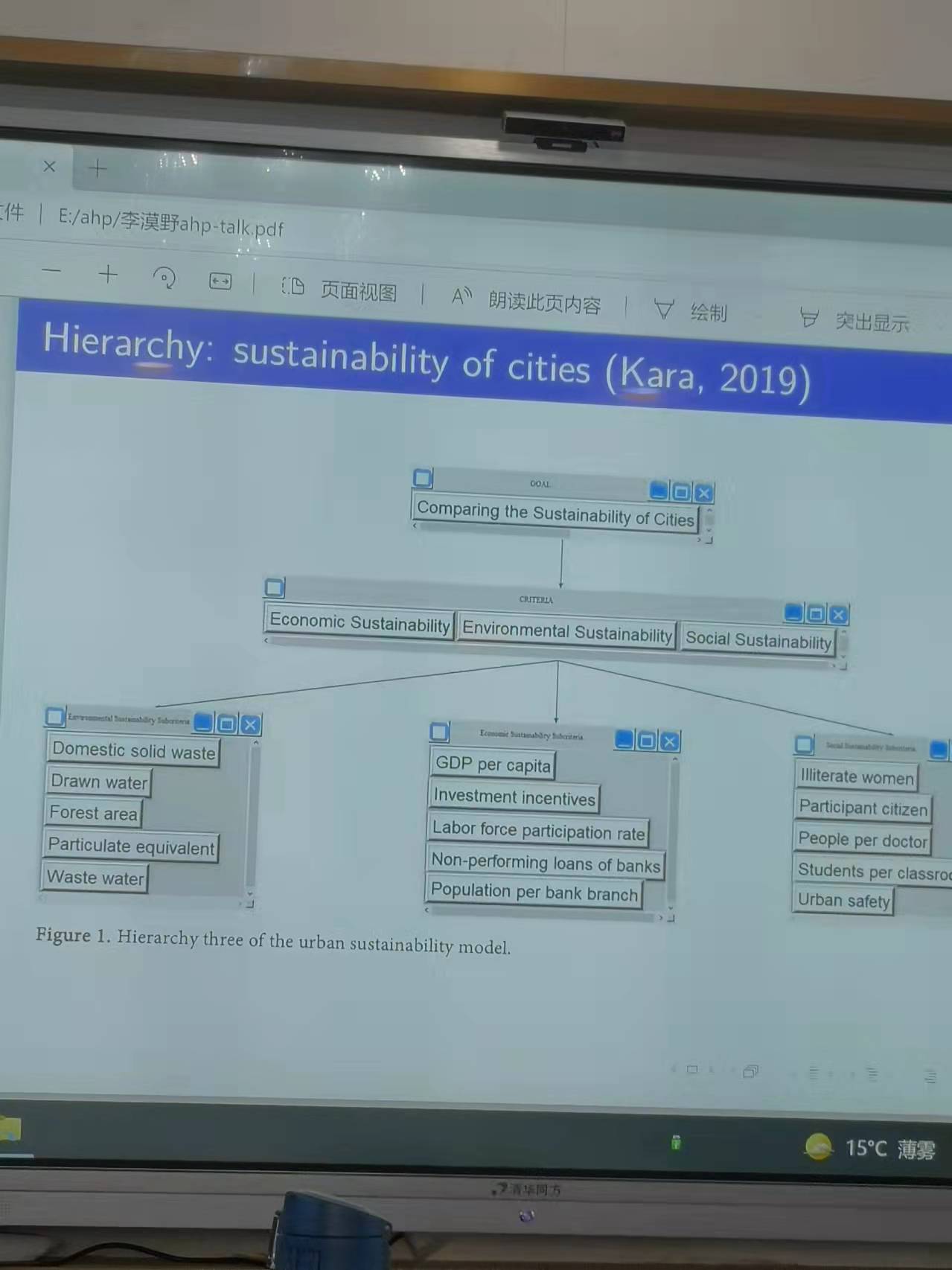
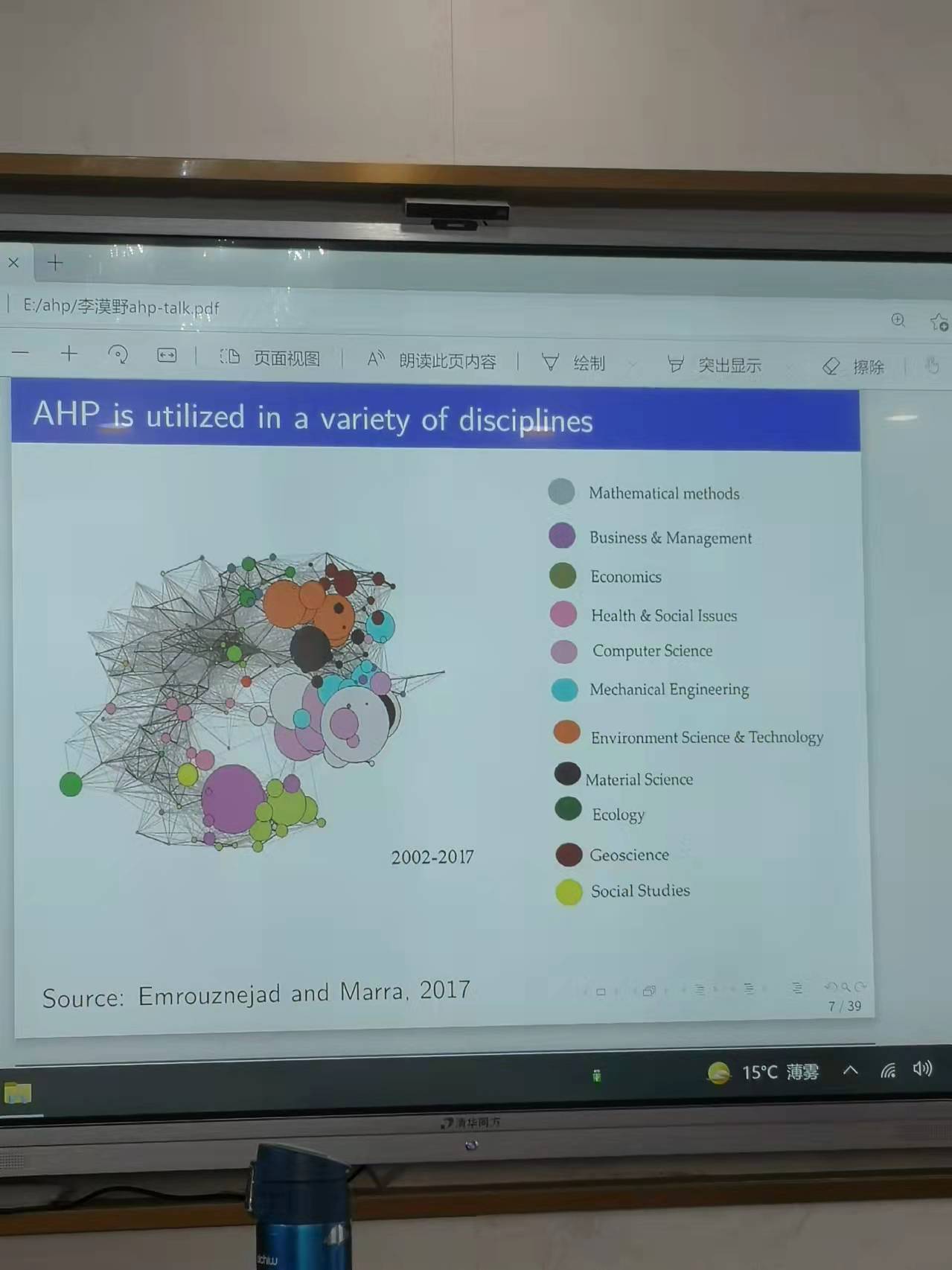
從文獻角度來看📤👧🏼,較為早期的研究的一個例子是假設考慮國家福利☣️,有三個因素可能會影響到國家的福利,包括經濟增長,環境質量以及國家安全問題,這三個問題導致能源需求的分配問題是可以使用層次分析法進行分解的。後人在前人的基礎上進行了拓展🏋🏿♀️,並將相關的問題拓展到微觀的供應商選擇問題之上🫑,假設選擇供應商首先考慮他們的績效,進而對服務進行分解,考慮第二層級的產品質量⛓、成本、運輸👻、以及服務,將產品質量分解成為第三層級的質量可靠性以及缺陷㊙️,成本分解為凈價格和物流成本等等,最終會對不同的供應商實現評價🚐。正因如此🧑🏻💼,層次分析法所能應用的領域是非常廣泛的🤚🏽,包括數學模型,商業管理,經濟學和環境科學💬。
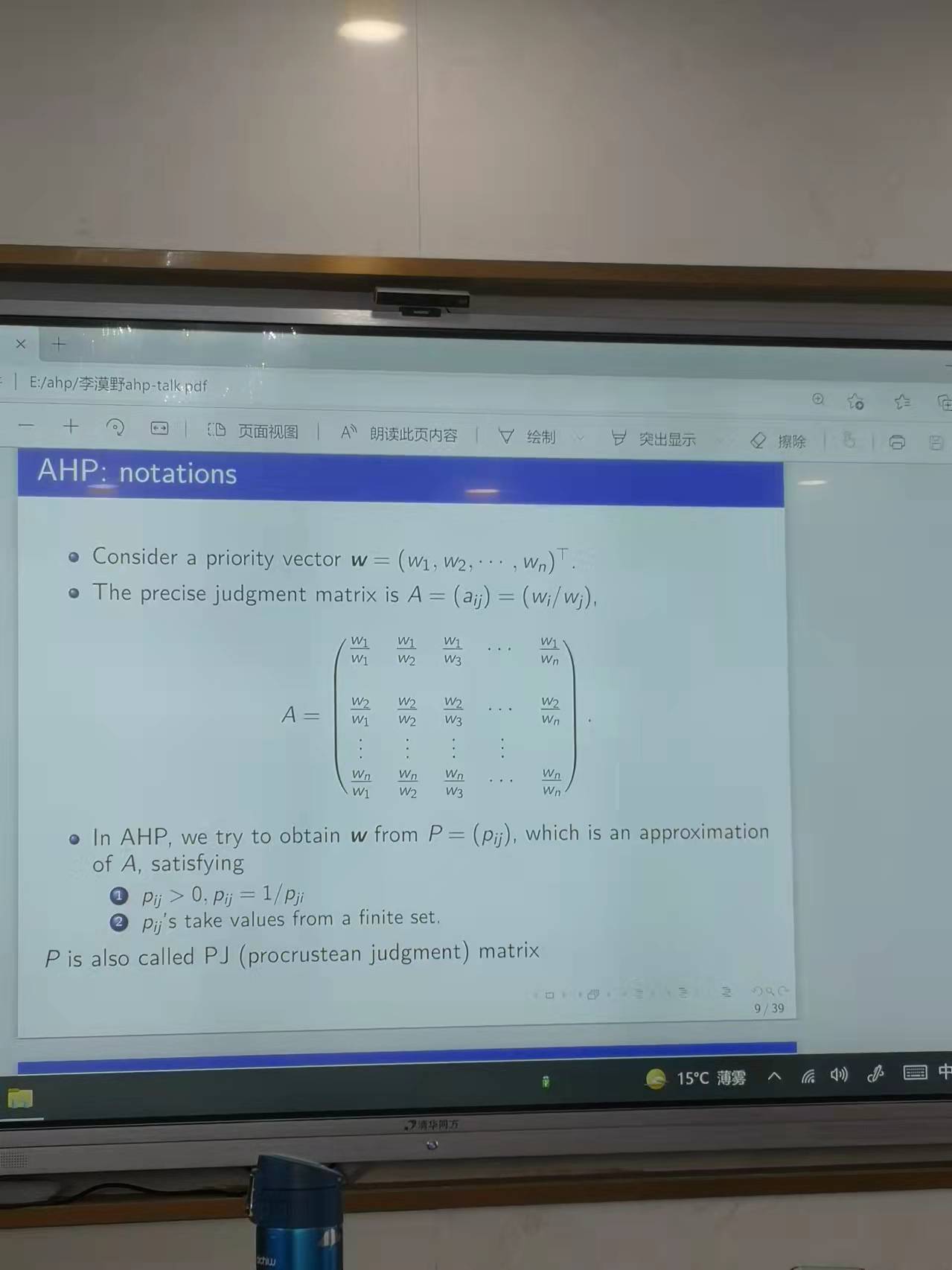
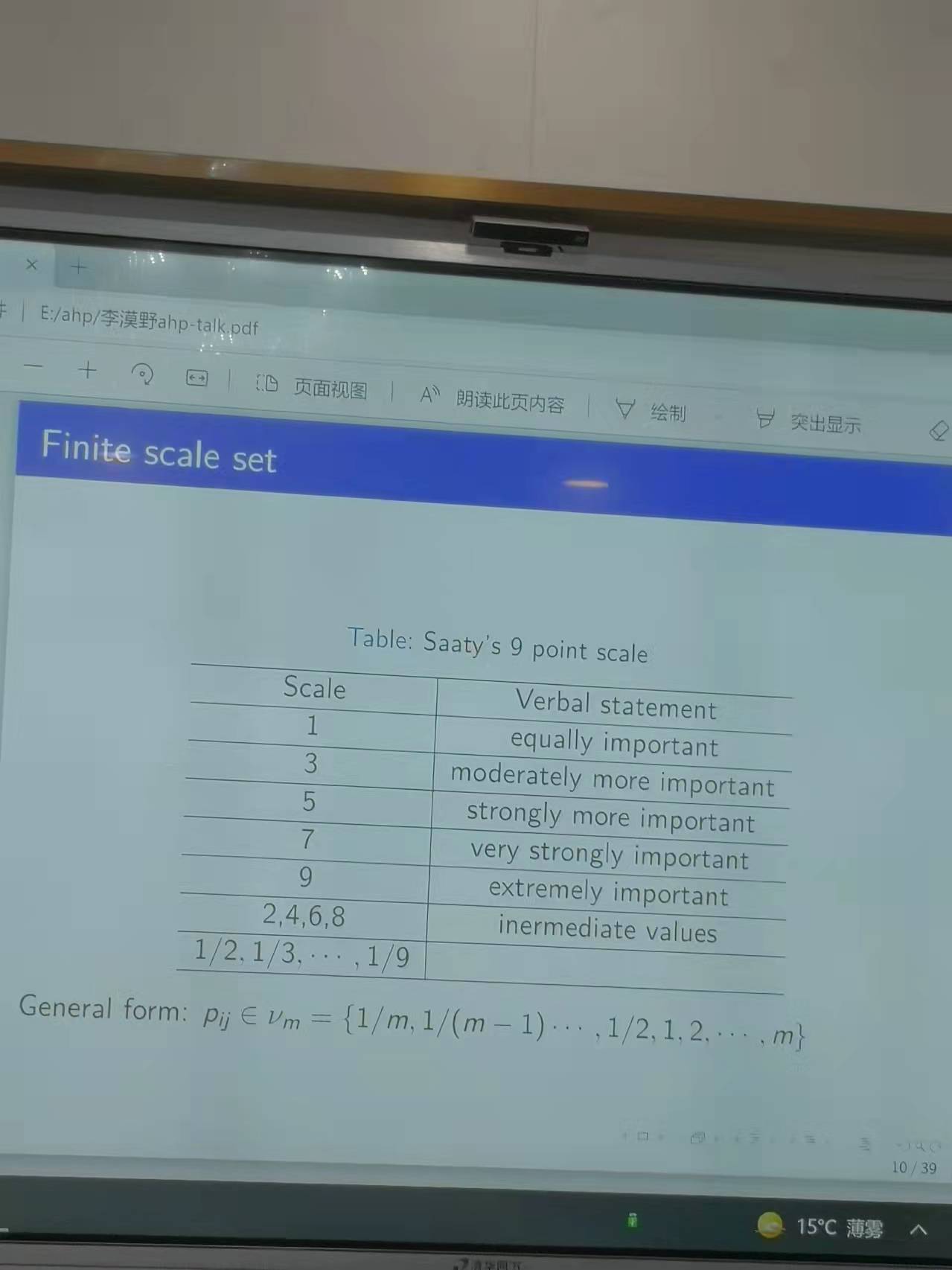
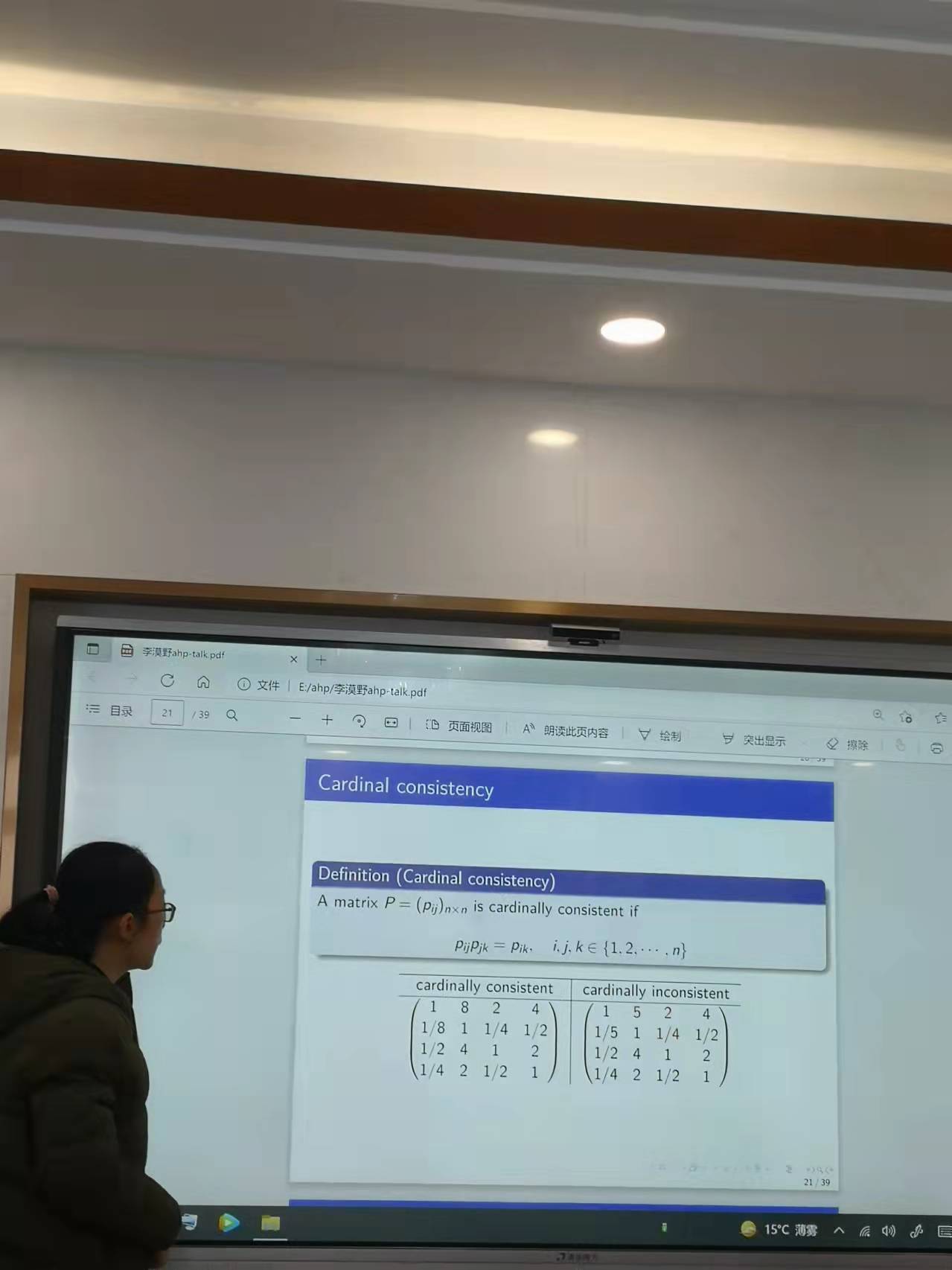
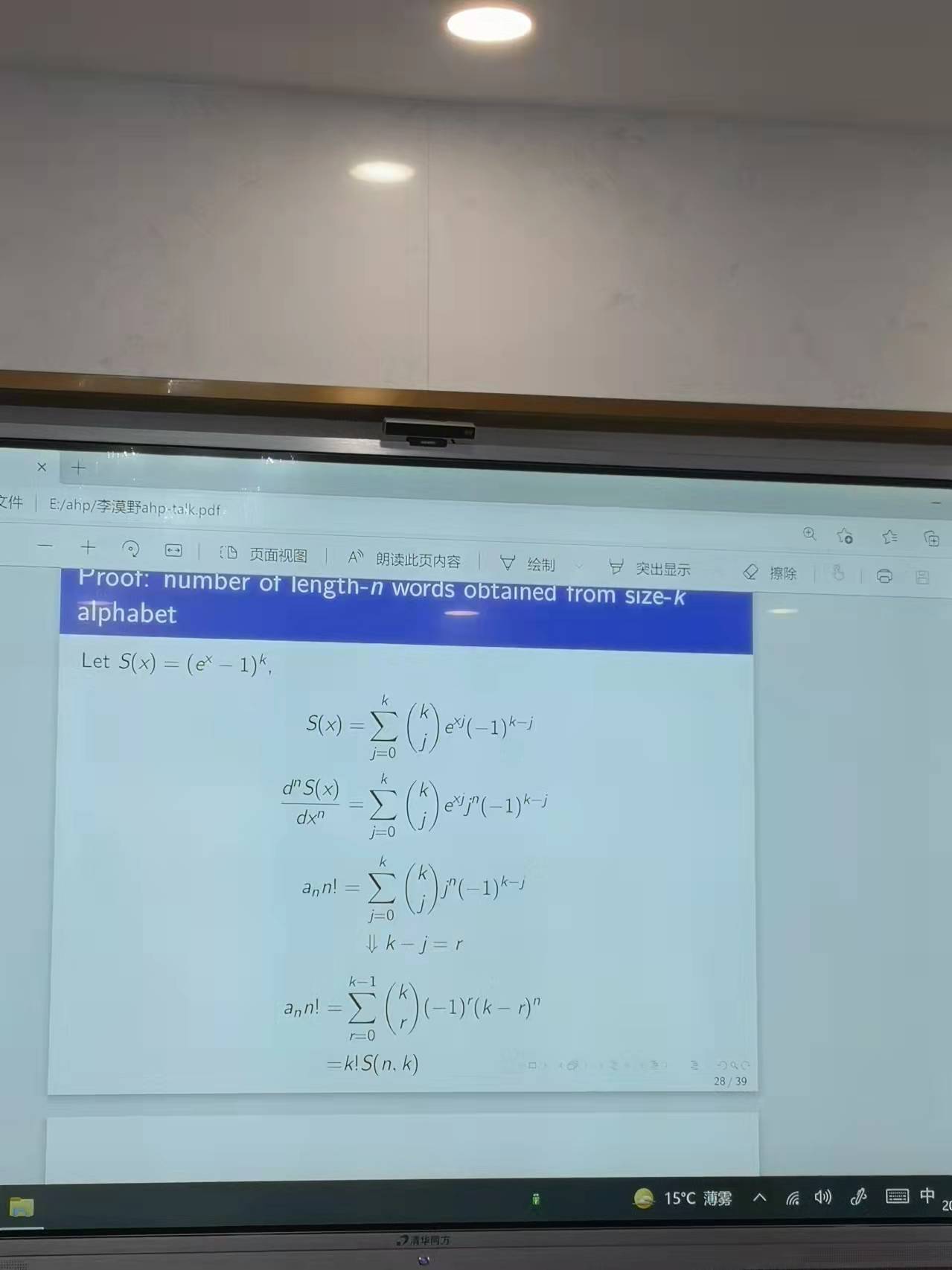
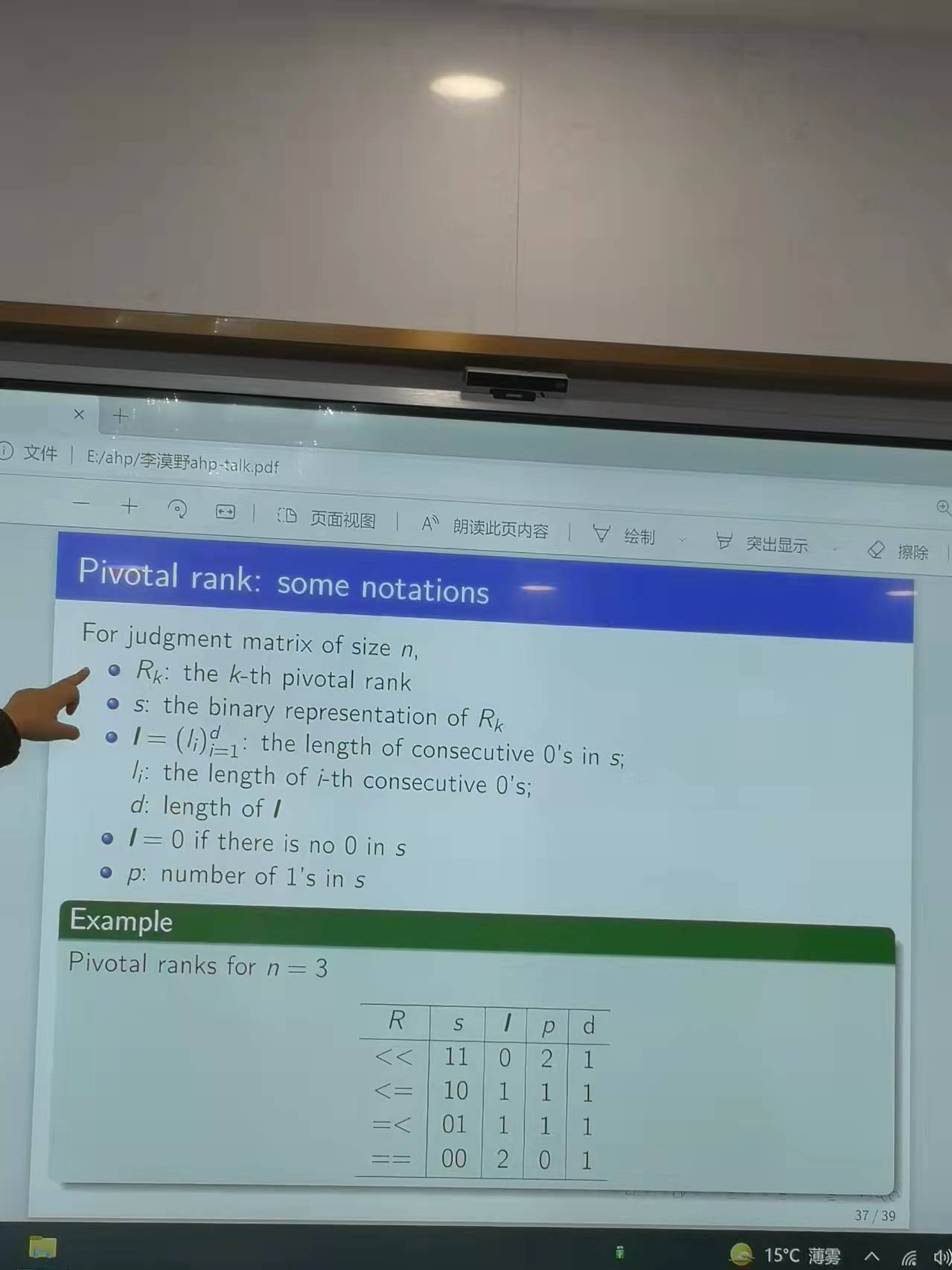
從層次分析法的方法論角度來看🧜♂️⏫,其首先假定一個主向量,為了達到兩兩比較的效果,使用每一行的行向量除以主向量,從而得到決策矩陣(Precise judgment matrix),在AHP的設計效果來看,評價標度主要是從一個有限的集合中取值🔽,從而得到不同的配對元素❎。這樣就得到了最終的PJ矩陣(procrustean judgment matrix)。一個例子是Saaty的分度表,其中使用離散數字1-9來表示某一標度的重要程度。從AHP實行的步驟上來看,AHP首先考慮建立層級(hierarchy),然後計算決策矩陣🕟,進行一致性檢驗,最終進行匯總。一致性檢驗基於決策一致性,一致性指數🥟,隨機指數和一致性比例,而在一致性指數設計中可能會涉及到求解矩陣的特征根問題,一致性比例從經驗要求來看,需要滿足一致性比例小於0.1🖐🏿。AHP進行的第四步是延展👨,其中包括Saaty提出的特征矢量方法🧑🏿🦳,Crawford提出的廣義平均方法🤜🏿,Zahedi提出的額外正則方法。隨後李老師舉了具體的例子說明一致性問題可能存在一致性和非一致性的兩個例子。隨著計算的頻率越高,其產生的矩陣越大,所以最終的AHP極有可能通過計算機來進行解決。因此,從這點來看,AHP方法極有可能是一個交叉學科問題。在實際問題的解決過程中,可以使用近似方法來提取AHP的主要的最大列,從而獲得相應的結果👨👧👧。李老師從組合數學的角度還列舉了兩個有意思的應用。從總量為K的字母表中生成一個長度為n的單詞,而所有的單詞至少被使用一次。如果對上述問題進行拓展👩🏽🍼,如果每個單詞至少出現b次,那麽從總量為K的單詞表中可能生成多少獨立的單詞。通過對問題分析並進行檢驗,從而可以對相關的問題進行了求解和拓展👫🏼。
李老師的講座給万达平台帶來了非常不一樣的知識延展,從而使組合數學和其他學科進行交叉具有了可能🚓,其所研究的問題如果進行深化,極有可能會得到非常重要的結果🤘🏽💾,希望李老師在科研和教學道路上不斷前行,為我們帶來更多的看世界的不一樣視角。



(供稿 曹煥)




