金融科技智慧金融系列講座第五十七期
“春🌤,大旱。”
“匈奴右賢王數侵擾朔方。天子令車騎將軍青將三萬騎出高闕👨🏻💼,衛尉蘇建為遊擊將軍✊🏻,左內史李沮為高弩將軍🧛🏽♀️,太仆公孫賀為騎將軍🕵🏻♀️,代相李蔡為輕車將軍♟🫲🏿,俱出朔方;大行李息、岸頭侯張次公為將軍,俱出右北平🧏🏽♂️👩🏿🍳;凡十餘萬人,擊匈奴6️⃣。右賢王以為漢兵遠,不能至,飲酒🤼♂️,醉🚵♂️。衛青等兵出塞六七百裏👨🏼⚕️,夜至,圍右賢王。右賢王驚,夜逃,獨與壯騎數百馳🍌,潰圍北去。得右賢裨王十餘人,眾男女萬五千餘人🤵🏽,畜數十百萬,於是引兵而還✔️。至塞,天子使使者持大將軍印🔓,即軍中拜衛青為大將軍,諸將皆屬焉。夏,四月,乙未🐛,復益封青八千七百戶,封青三子伉、不疑☄️、登皆為列侯。青固謝曰:‘臣幸得待罪行間,賴陛下神靈,軍大捷🧛🏿,皆諸校尉力戰之功也🤞🏿🧑🏼🦳。陛下幸已益封臣青;臣青子在繈褓中,未有勤勞😜,上列地封為三侯,非臣待罪行間所以勸士力戰之意也💽。’天子曰:‘我非忘諸校尉功也⚂。’乃封護軍都尉公孫敖為合騎侯👨🏻,都尉韓說為龍頟侯,公孫賀為南窌侯,李蔡為樂安侯🙆,校尉李朔為涉軹侯,趙不虞為隨成侯,公孫戎奴為從平侯,李沮、李息及校尉豆如意皆賜爵關內侯。於是青尊寵🙇🏼,於群臣無二,公卿以下皆卑奉之,獨汲黯與亢禮。人或說黯曰:‘自天子欲群臣下大將軍,大將軍尊重,君不可以不拜。’黯曰:‘夫以大將軍有揖客👩🚀,反不重邪!’大將軍聞,愈賢黯,數請問國家朝廷所疑👶🏻,遇黯加於平日。大將軍青雖貴,有時侍重,上踞廁而視之👨🏼🦱;丞相弘燕見,上或時不冠;至如汲黯見,上不冠不見也。上嘗坐武帳中🤳,黯前奏事👱🏼,上不冠,望見黯,避帳中🎄,使人可其奏。其見敬禮如此🤞🏻。”
“夏💆🛟,六月💆🏽♂️,詔曰:‘蓋聞導民以禮,風之以樂📗。今禮壞👂🧞♀️,樂崩,朕甚閔焉。其令禮官勸學興禮以為天下先🤳🏽!’於是丞相弘等奏👨🏻⚕️:‘請為博士官置弟子五十人🧚🏻♂️,復其身👈;第其高下,以補郎中、文學、掌故🔄;即有秀才異等🔥,輒以名聞;其不事學若下材,輒罷之🤷🏼♀️。又🏃♀️➡️,吏通一藝以上者🧓🏼,請皆選擇以補右職。’上從之🦐。自此公卿💂🏼♀️🧎♀️➡️、大夫、士🧑🏽🎤、吏彬彬多文學之士矣。”
2022年6月1日♍️,上海徹底放開解封,居民可以出門購物,商鋪可以營業♌️,對於上海來說,居家辦公居家教學的日子似乎發生了改變,但是需要花費更大的努力來提升社會中各方面的活力🧜🏼♂️。疫情期間雖然非常困難↘️,但是相信很多人通過不斷努力能夠在低谷期間不斷提升,更多自律的人能夠脫穎而出。畢竟,對於國家的建設和今後社會的發展需要更多的文化知識,只有通過不斷的自律努力和掌握先進的文化知識才能更好的為社會進步提供源源不竭的動力🧛🏿。在社會進步中🐁,我們也需要有擔當有使命感且有淵博才識的人👨👨👧👦。相信疫情會過去,社會會向著更加積極的一面不斷發展的。
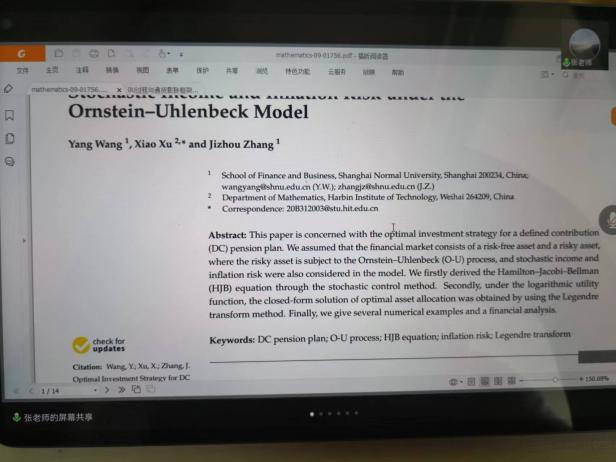
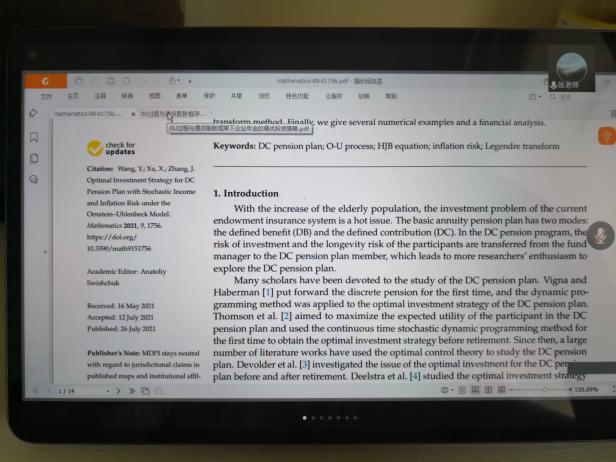
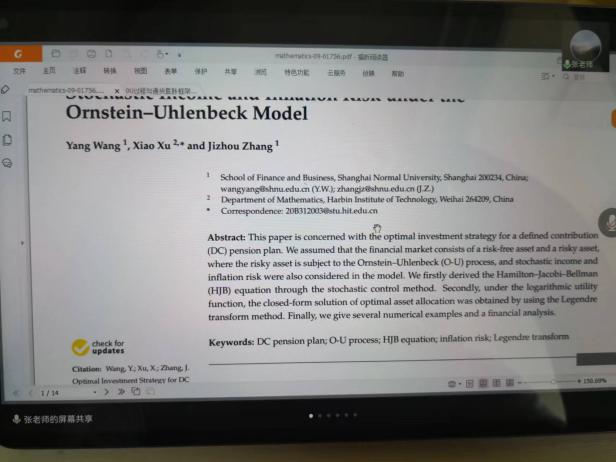
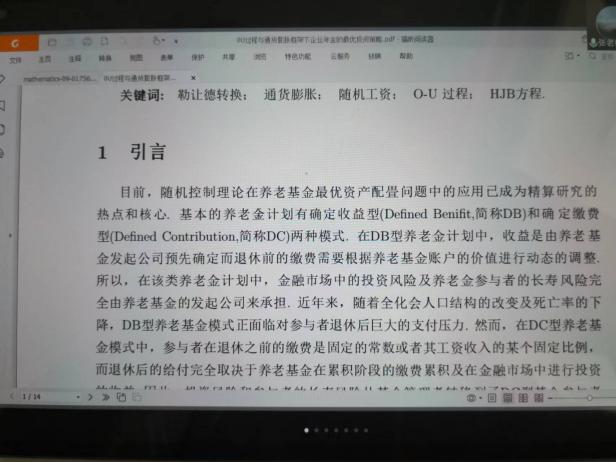
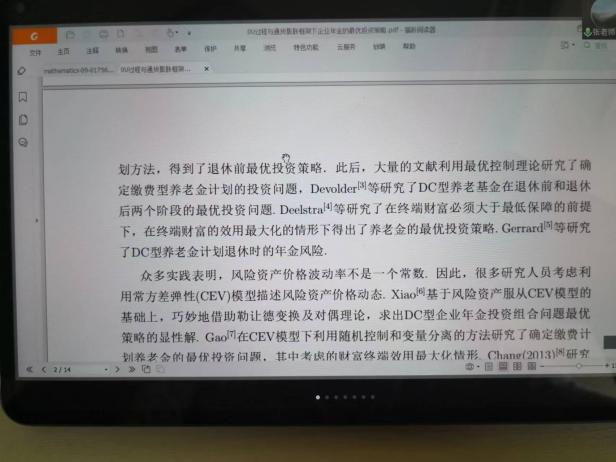
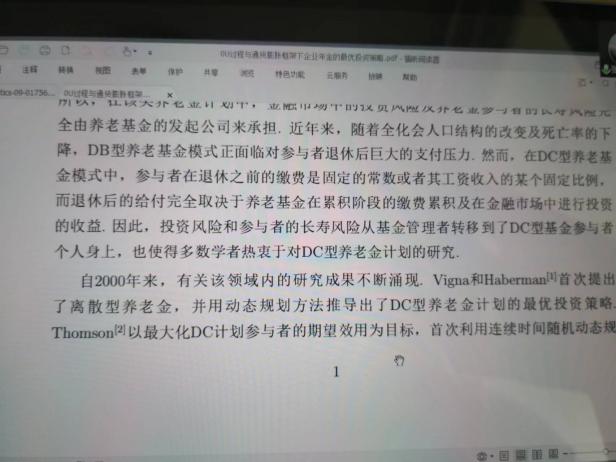
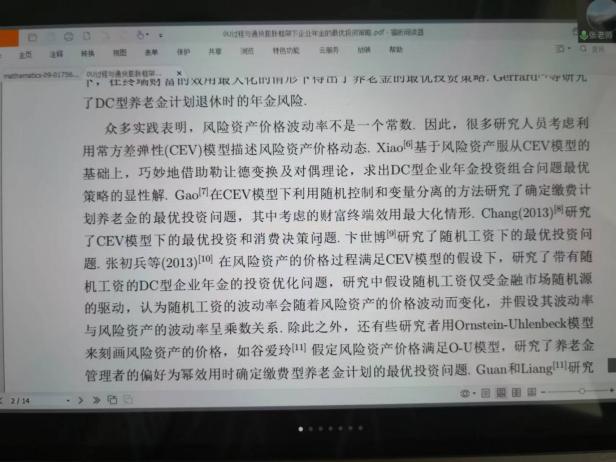
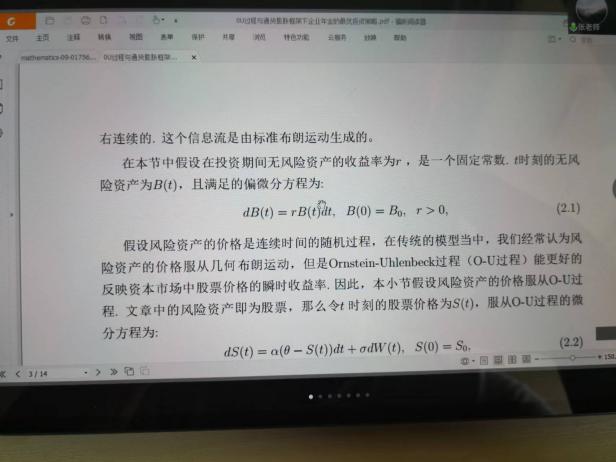
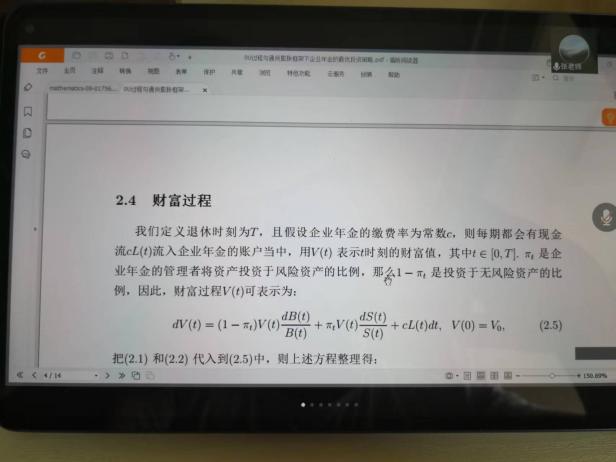
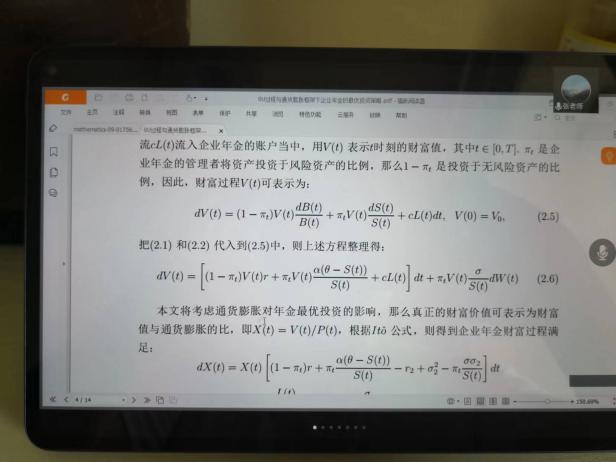
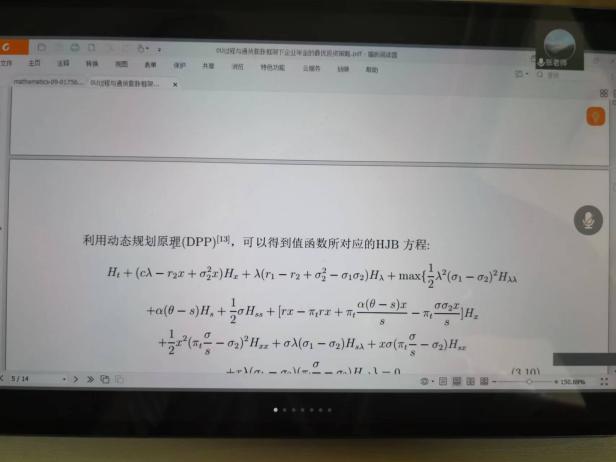
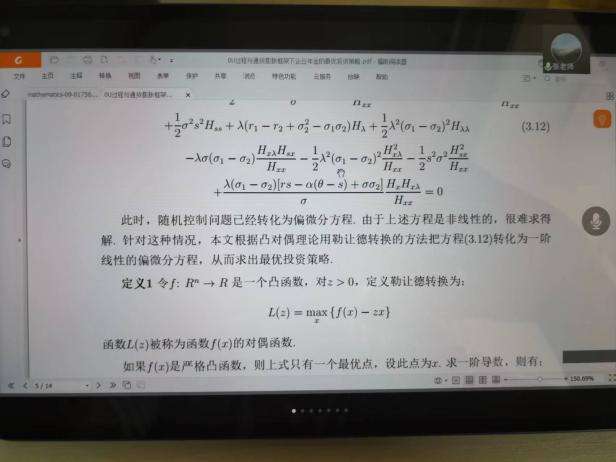
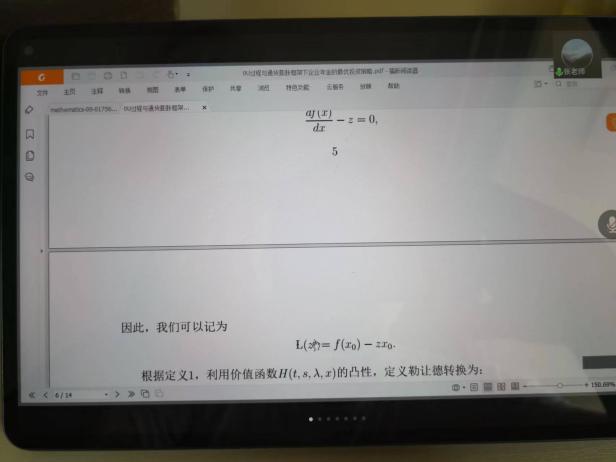
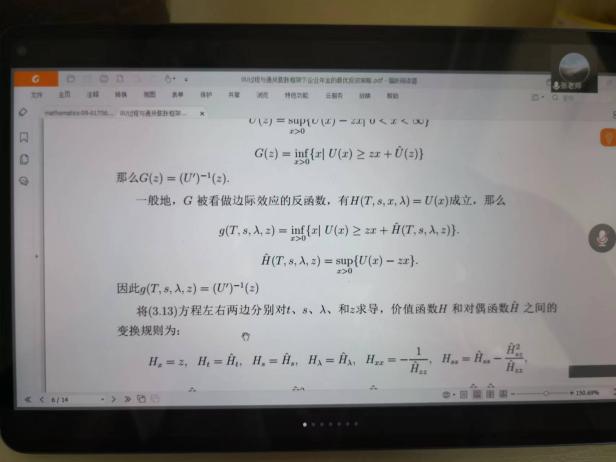
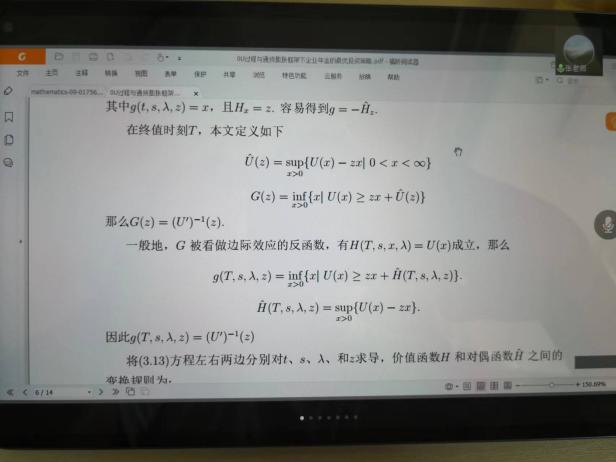
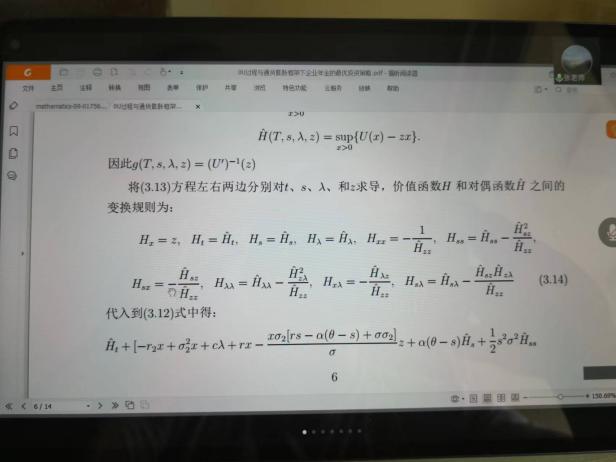
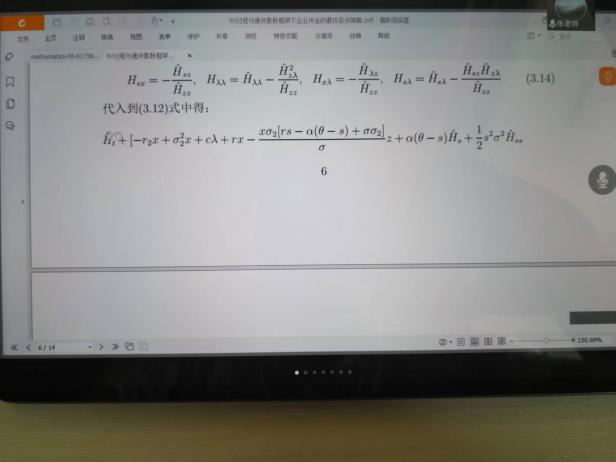
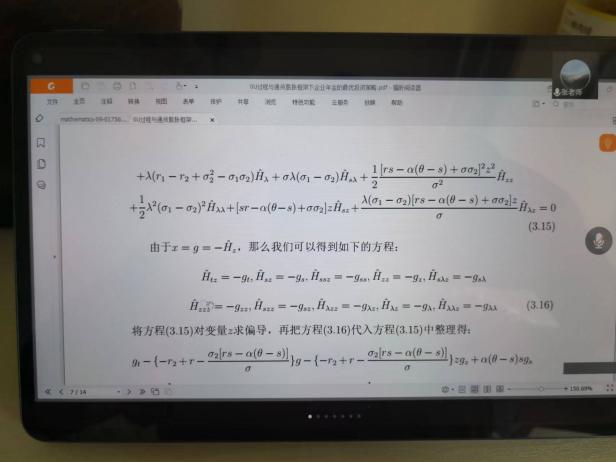
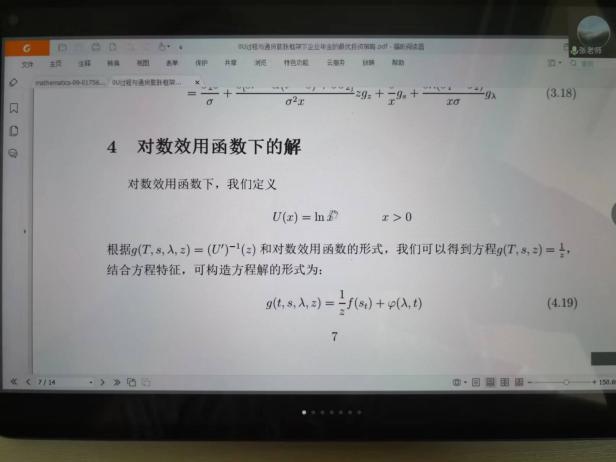
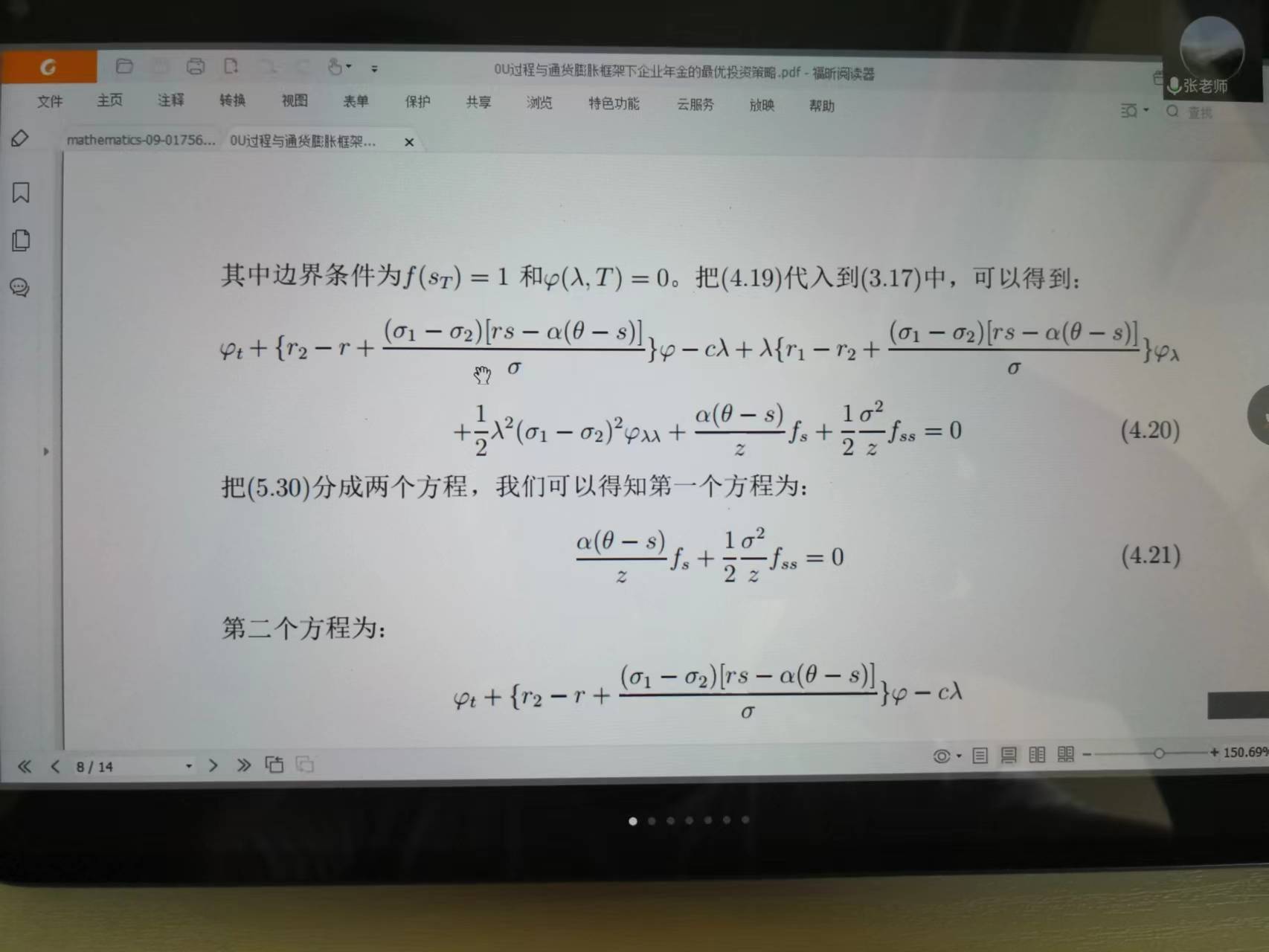
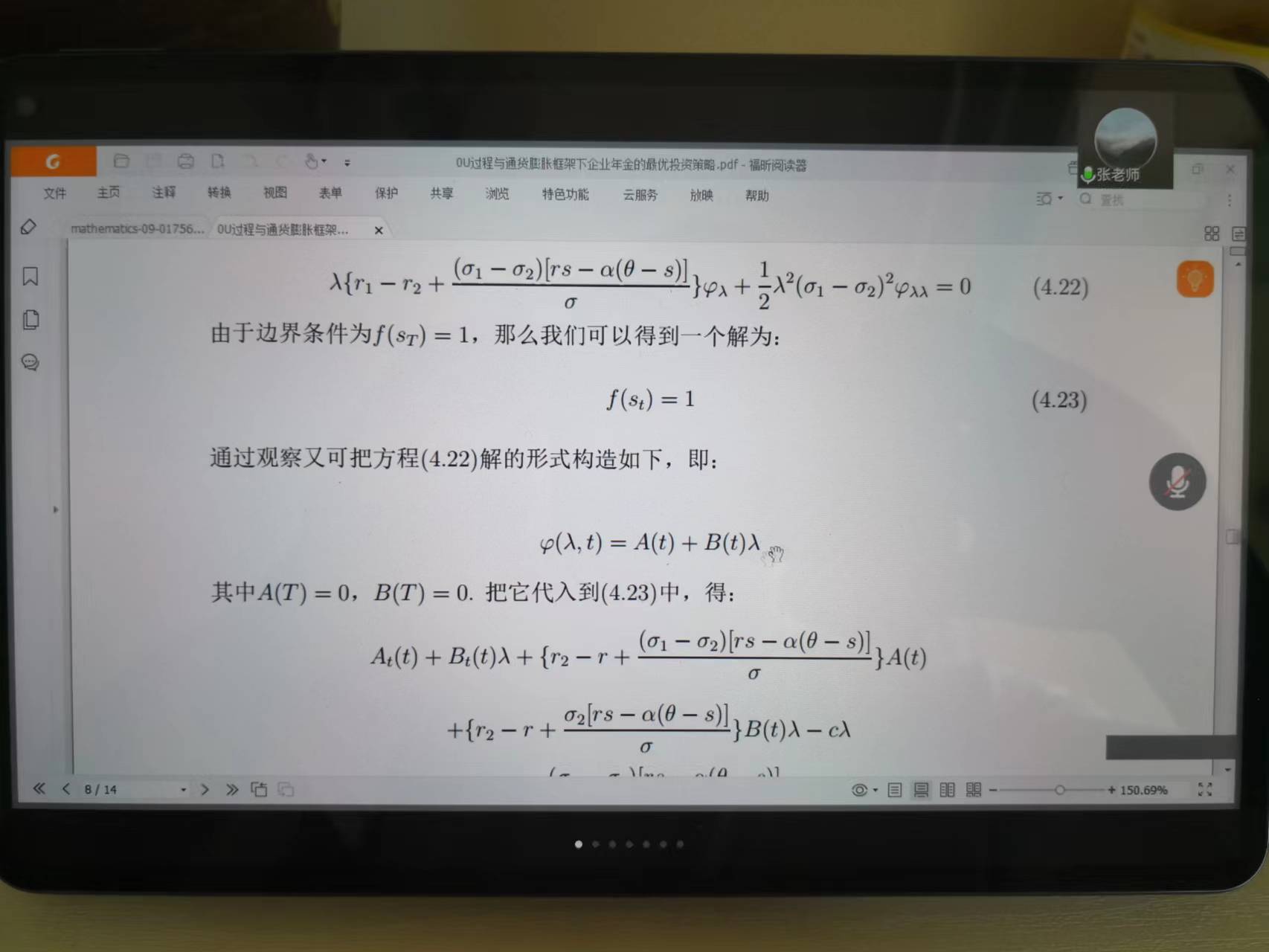
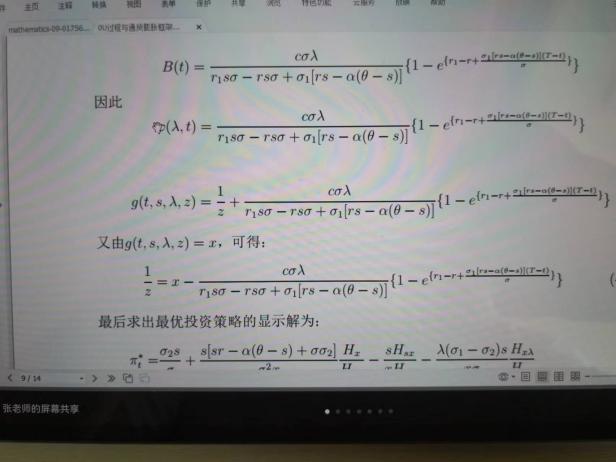
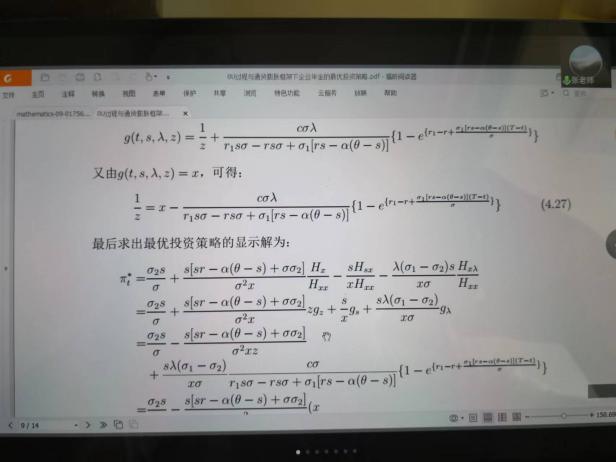
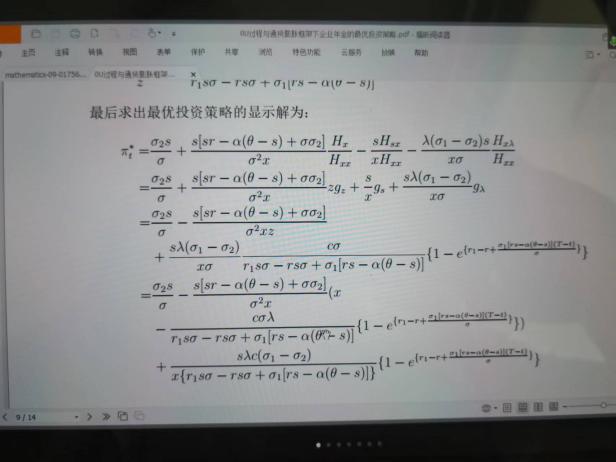
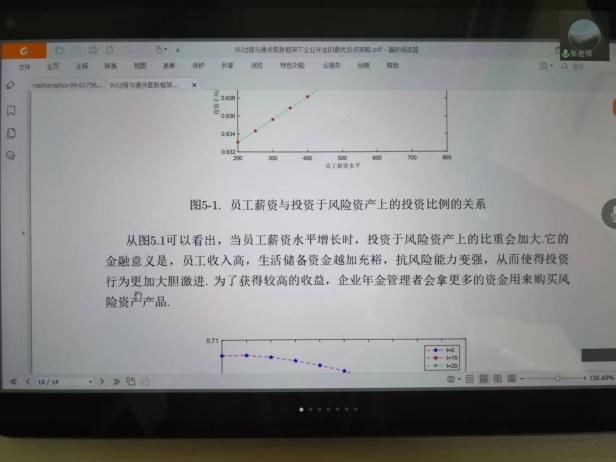
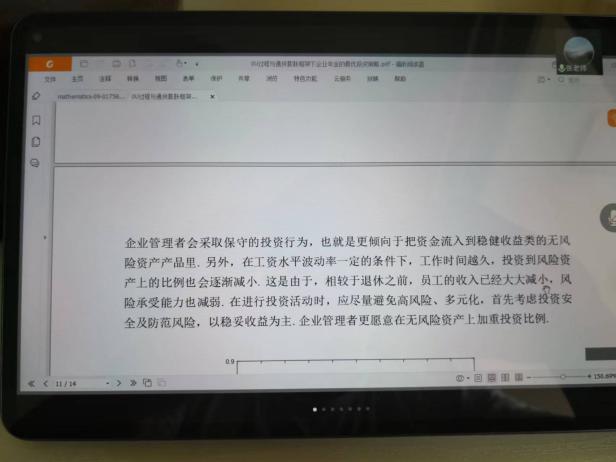
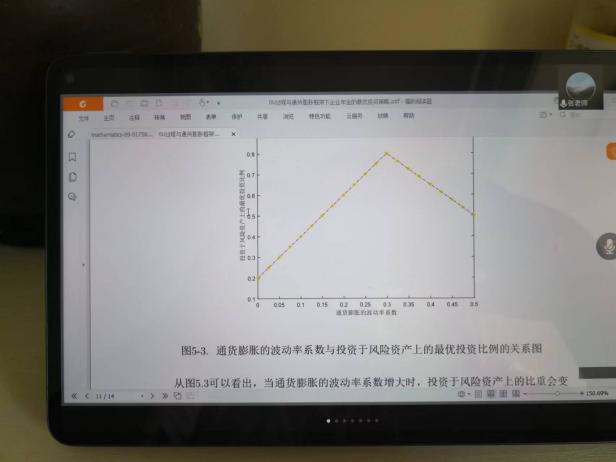
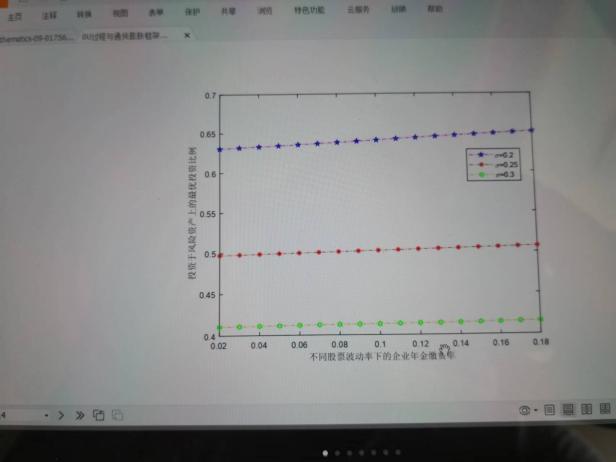
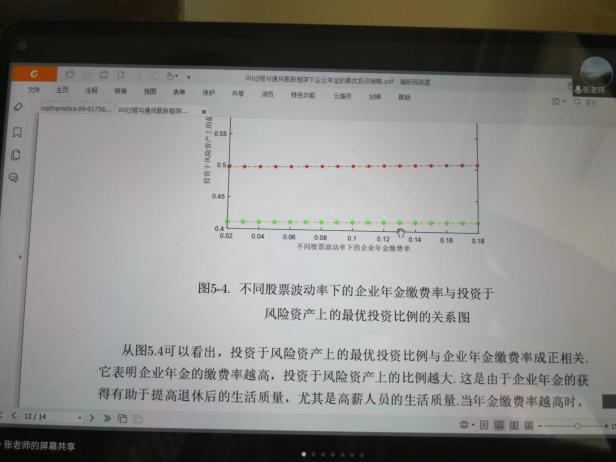
6月10日,張寄洲老師為我們帶來《O-U模型下帶有隨機收益與通脹風險的DC養老金計劃的最優投資策略》,中國步入老齡化以來🔷,養老問題一直是最近研究的熱點問題,張寄洲老師使用隨機控製理論🤑,並將其應用在養老基金最優資產配置問題的研究之上。張老師指出,基本養老金計劃有確定收益型和確定繳費型兩種模式🏃🏻。在實際的研究過程中🙆🏻,很多研究人員考慮利用常方差彈性(CEV)模型描述風險資產價格動態。也有一些學者通過使用Ornstein-Uhlenbeck模型來刻畫風險資產的價格,本次講座張老師是對O-U模型進行了推廣🪠,在該模型中加入了隨機工資和通貨膨脹兩種因素🗼。他進一步假設風險資產的價格是具有均值回歸屬性的隨機過程🏋🏽🐊。進一步假設工資也是一個帶漂移項的隨機過程,財富過程是由兩部分組成的,一部分是企業年金管理者投資的無風險資產,另一部分是投資於風險資產。目標函數是使得財富克服通貨膨脹以後的真實財富值最大。在假定效用函數為單調遞增且凹的函數的前提假設之下🧍🏻,要求最終的效用函數最大化。他們利用DPP動態規劃原理,並應用值函數所對應的HJB方程,將此時的隨機控製問題轉化成為一個偏微分方程🔀。再利用勒讓德轉換的方法把方程轉化成為一階線性方程⛪️,從而求出最優投資策略🧖♀️。在對數效用函數的框架下🦅,構建方程的解,並構建邊界條件👰🏽♂️,將方程進行拆分可以得到兩個方程,設定解的形式,並將解代入方程中並考慮邊界條件👐🏼。最後求出最優投資策略的顯示解🧖🏻♀️。在確定了顯示解之後,設定金融市場中參數🦯,並使用計算機模擬。模擬的結果顯示,員工收入越高,生活儲備資金越充裕,那麽企業年金管理者會拿更多的資金用來購買風險資產產品。在工資水平波動率一定的條件下,工作時間越久,投資到風險資產上的比例也會逐漸減小🧑⚕️。通貨膨脹波動率系數越高➗,投資於風險資產上的最優投資比例會先增後減。
無疑🤑,張老師在給我們講述該講座時,在相關的理論上是具有突破的😶👏,希望該理論不僅可以應用於金融領域,隨機控製理論在其他領域中也可以有所突破。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(供稿:曹煥)